Beyond the quantum Limit

When a metal is subject to magnetic field, the electron trajectories are helices spiraling around the field lines, here defined as "Landau tubes". As the magnetic field increases, the diameter of this Landau tube decreases . When this diameter becomes comparable to the Fermi wave length the quantum limit is attained. This is an exciting playground for scientist to explore an extreme manifestation of quantum mechanics in the behavior of electrons.

Unfortunately, this quantum limit is still out of reach for a standard 3D metal with current magnetic field technology. The typical highest magnetic field available is around 70T in pulsed magnet facilities (for more information about this technology have a look on http://www.toulouse.lncmi.cnrs.fr/spip.php?article102&lang=en). In the case of the copper, the magnetic field required to reach the quantum limit would be several 10kT! However, this limit is lower in the case of a semi-metal such as bismuth and graphite for which this limit is reached for a field of few Tesla.

The case of bismuth

Our investigation of the thermoelectric response revealed that the most sensitive probe of the quantum oscillation phenomena in the quantum limit of semi metals is the Nernst effect[1,2,3,6]. Using this probe, we explored the Landau level diagram of the Dirac electron in bismuth up to 28T. As an illustration, we reported on Fig.1 the rich Landau level spectrum of bismuth closed the trigonal axis.

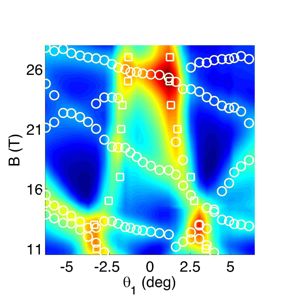
Fig.1 : Color plot of the angular Nernst voltage for a magnetic field oriented in the (trigona,binary) plane. Blue to red transition indicates variation from the minimum to maximum. Nernst peaks resolved in S xy ( B ) ( S xy ( θ1 )) sweeps are marked by circles (squares).

The case of graphite

In the case of graphite, it is known since the 80’s that a large magnetic field apply along the c-axis modify the electronic ground state. In collaboration with the group of C.Proust and as illustrated on Fig.2, we extended the investigation of the quantum limit of graphite up to 80T. We found a second transition induced by the magnetic field. These unexpected transitions are accompanied by the opening of a gap along the c-axis. Surprisingly, the electrons remain metallic in the plane in spite of a fully gap electronic spectrum. Such paradoxical behavior underline the complexity of the electronic organization in the quantum limit regime which the subject of our research. Recently, in collaboration with D. LeBoeuf from LNCMI-Grenoble, we idientified the firt thermodynamical signature of these transitions.

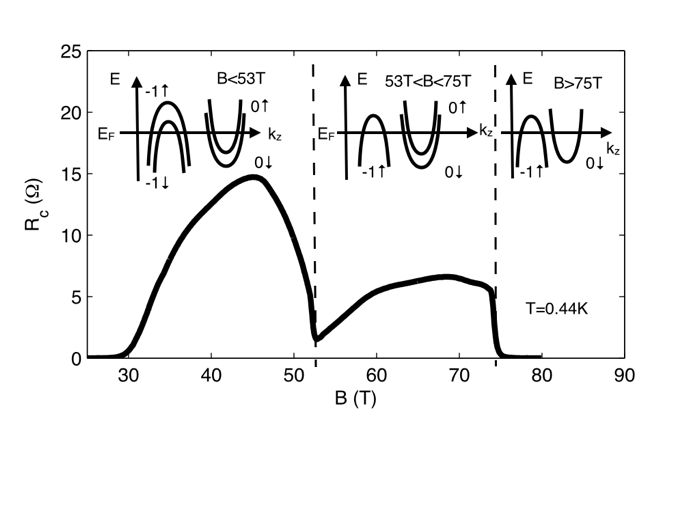
Fig.2 : Field dependence of the out-of-plane resistance Rc of
kish graphite (sample K3) at T = 0.44 K (black line).

Reference :
[1] Oscillating Nernst-Ettingshausen effect in Bismuth across the quantum limit
Kamran Behnia, Marie-Aude Miasson and Yakov Kopelevich
Phys. Rev. Lett. 98, 166602 (2007)

[2] Nernst effect in semi-metals: the meritorious heaviness of electrons
Kamran Behnia, Marie-Aude Miasson and Yakov Kopelevich
Phys. Rev. Lett. 98, 076603 (2007)

[3]Nernst effect and dimensionality in the quantum limit
Zengwei Zhu, Huan Yang, Benoît Fauqué, Yakov Kopelevich, Kamran Behnia
Nature Physics 6, 26-29 (8 November 2009) doi:10.1038/nphys1437

[4] Signatures of Electron Fractionalization in Ultraquantum Bismuth
Kamran Behnia, Luis Balicas, Yakov Kopelevich
Sicence 317. no. 5845, pp. 1729 - 1731 (2007)

[5] Phase diagram of bismuth in the extreme quantum limit
Huan Yang, Benoît Fauqué, Liam Malone, Arlei B. Antunes, Zengwei Zhu, Ctirad Uher and Kamran Behnia,
Nature Com 1,41 (2010)

[6] Transport anomalies across the quantum limit in semimetallic Bi0.96Sb0.04
A.Banerjee, B. Fauqué, K. Izawa, A. Miyake, I.Sheikin, J.Flouquet, B. Lenoir, K. Behnia
Rapid Comm. Phys. Rev. B, 78, 161103 (2008)

[7] Two Phase Transitions Induced by a Magnetic Field in Graphite
Benoît Fauqué, David LeBoeuf, Baptiste Vignolle, Marc Nardone, Cyril Proust, and Kamran Behnia
Phys. Rev. Lett. 110, 266601 (2013)

[8] Thermodynamic signatures of the field-induced states of graphite
D. LeBoeuf, C. W. Rischau, G. Seyfarth, R. Küchler, M. Berben, S. Wiedmann, W. Tabis, M. Frachet, K. Behnia, B. Fauqué
Nature Communications, 8 (1), 1-6 (2017)